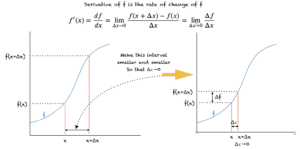
In very simple words, the derivative of a function f(x) represents its rate of change and is denoted by either f’(x) or df/dx. Let’s first look at its definition and a pictorial illustration of the derivative.
Illustration of the Definition of a Function Derivative
In the figure, Δx represents a change in the value of x. We keep making the interval between x and (x+Δx) smaller and smaller until it is infinitesimal. Hence, we have the limit (Δ𝑥→0). The numerator f(x+Δx)-f(x) represents the corresponding change in the value of the function f over the interval Δx. This makes the derivative of a function f at a point x, the rate of change of f at that point.
An important point to note is that Δx, the change in x can be negative or positive. Hence:
0<|Δx|< 𝜖,
where 𝜖 is an infinitesimally small value.
About the Notation
The derivative of a function can be denoted by both f’(x) and df/dx. The mathematical giant Newton used f’(x) to denote the derivative of a function. Leibniz, another mathematical hero, used df/dx. So df/dx is a single term, not to be confused with a fraction. It is read as the derivative of a function f with respect to x, and also indicates that x is the independent variable.
Connection with Velocity
One of the most commonly cited examples of derivatives is that of velocity. Velocity is the rate of change of distance w.r.t. time. Hence if f(t) represents the distance travelled at time t, then f’(t) is the velocity at time t. The following sections show various examples of computing the derivative.