All Courses
AI Career Planner
1:1 Coaching/Mentoring
Job Board
SQL
HTML/CSS/JS
Coding
Settings
LogoutWhat are Entropy and Information gain in Decision tree algorithm?
Defining Entropy
“What is entropy?” In the Lyman words, it is nothing just the measure of disorder, or measure of purity. Basically, it is the measurement of the impurity or randomness in the data points.
A high order of disorder means a low level of impurity, let me simplify it. Entropy is calculated between 0 and 1 , although depending upon the number of groups or classes present in the data set it could be larger than 1 but it signifies the same meaning, i.e. higher level of disorder.
For the sake of simple interpretation, let us confine the value of entropy between 0 and 1.
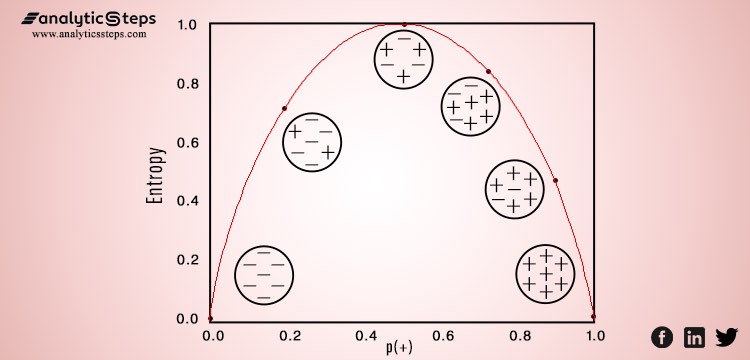
In the below image, an inverted “U” shape depicts the variation of entropy on the graph, the x-axis presents data points and the y-axis shows the value of entropy. Entropy is the lowest (no disorder) at extremes (both end) and maximum (high disorder) in the middle of the graph.
Variation of entropy against data points
“Entropy is a degree of randomness or uncertainty, in turn, satisfies the target of Data Scientists and ML models to reduce uncertainty.”
What is Information Gain?
The concept of entropy plays an important role in calculating Information Gain.
Information Gain is applied to quantify which feature provides maximal information about the classification based on the notion of entropy, i.e. by quantifying the size of uncertainty, disorder or impurity , in general, with the intention of decreasing the amount of entropy initiating from the top (root node) to bottom(leaves nodes).
The information gain takes the product of probabilities of the class with a log having base 2 of that class probability, the formula for Entropy is given below:
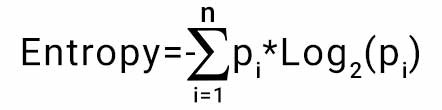
Entropy Formula
Here “p” denotes the probability that it is a function of entropy.