All Courses
AI Career Planner
1:1 Coaching/Mentoring
Job Board
SQL
HTML/CSS/JS
Coding
Settings
LogoutNormal (Gaussian) Distributions
Suppose we were interested in characterizing the variability in body weights among adults in a population. We could measure each subject’s weight and then summarize our findings with a graph that displays different body weights on the horizontal axis (the X-axis) and the frequency (% of subjects) of each weight on the vertical axis (the Y-axis) as shown in the illustration on the left. There are several noteworthy characteristics of this graph. It is bell-shaped with a single peak in the center, and it is symmetrical. If the distribution is perfectly symmetrical with a single peak in the center, then the mean
value, the mode, and the median will be all be the same. Many variables have similar characteristics, which are characteristic of so-called normal or Gaussian distributions. Note that the horizontal or X-axis displays the scale of the characteristic being analyzed (in this case weight), while the height of the curve reflects the probability of observing each value. The fact that the curve is highest in the middle suggests that the middle values have higher probability or are more likely to occur, and the curve tails off above and below the middle suggesting that values at either extreme are much less likely to occur. There are different probability models for continuous outcomes, and the appropriate model depends on the distribution of the outcome of interest. The normal probability model applies when the distribution of the continuous outcome conforms reasonably well to a normal or Gaussian distribution, which resembles a bell shaped curve. Note normal probability model can be used even if the distribution of the continuous outcome is not perfectly symmetrical; it just has to be reasonably close to a normal or Gaussian distribution.
Skewed Distributions
However, other distributions do not follow the symmetrical patterns shown above. For example, if we were to study hospital admissions and the number of days that admitted patients spend in the hospital, we would find that the distribution was not symmetrical, but skewed. Note that the distribution to the distribution below is not symmetrical, and the mean value is not the same as the mode or the median.
Characteristics of Normal Distributions
Distributions that are normal or Gaussian have the following characteristics:
- Approximately 68% of the values fall between the mean and one standard deviation (in either direction)
- Approximately 95% of the values fall between the mean and two standard deviations (in either direction)
- Approximately 99.9% of the values fall between the mean and three standard deviations (in either direction)
If we have a normally distributed variable and know the population mean (μ) and the standard deviation (σ), then we can compute the probability of particular values based on this equation for the normal probability model:
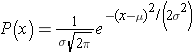
where μ is the population mean and σ is the population standard deviation. (π is a constant = 3.14159, and e is a constant = 2.71828.) Normal probabilities can be calculated using calculus or from an Excel spreadsheet.