Explain the Bayes theorem

Data Science, AI and ML
, ,
#1

Bayes theorem

#2

P(A|B)=P(B|A)P(A)/P(B) where A and B are two events, P(B|A) is the probability of getting B such that Event A has already occurred.

#3

This is Bayes’ Theorem:

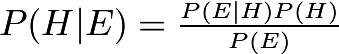
main-qimg-1aafaadb7ca5e7c862f3def633ed013b

It allows you to find a conditional probability or update your belief after you gather more data.

It is useful in many areas and points out one problem that some people have with probabilities. They get confused between the probability of A given B and the probability of B given A. Some examples:

Let A = “is a White American man” and B = “is a senator in the USA”. Now, 𝑃(𝐴|𝐵)P(A|B) is quite high, I forget how high right now, but about 0.9. But 𝑃(𝐵|𝐴)P(B|A) is quite small, about 0.00000009.