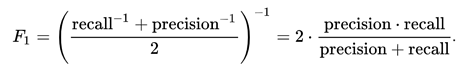In the last section, we discussed precision and recall for classification problems and also highlighted the importance of choosing precision/recall basis our use case. What if for a use case, we are trying to get the best precision and recall at the same time? F1-Score is the harmonic mean of precision and recall values for a classification problem. The formula for F1-Score is as follows:
Now, an obvious question that comes to mind is why are taking a harmonic mean and not an arithmetic mean. This is because HM punishes extreme values more. Let us understand this with an example. We have a binary classification model with the following results:
Precision: 0, Recall: 1
Here, if we take the arithmetic mean, we get 0.5. It is clear that the above result comes from a dumb classifier which just ignores the input and just predicts one of the classes as output. Now, if we were to take HM, we will get 0 which is accurate as this model is useless for all purposes.
This seems simple. There are situations however for which a data scientist would like to give a percentage more importance/weight to either precision or recall. Altering the above expression a bit such that we can include an adjustable parameter beta for this purpose, we get:
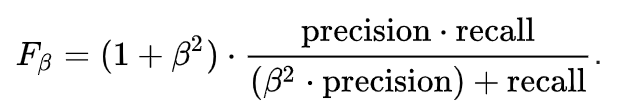
Fbeta measures the effectiveness of a model with respect to a user who attaches β times as much importance to recall as precision.