Data Structures: Stacks and Queues

Software Development
#1

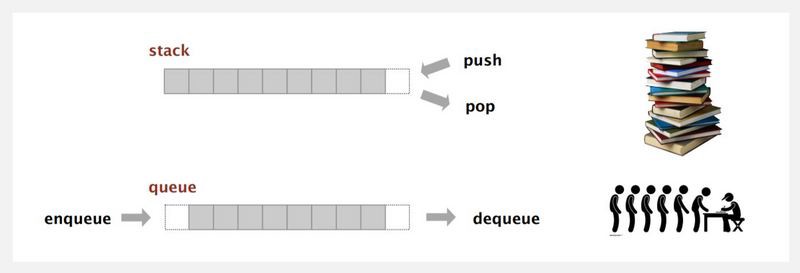
Definition

Both Stacks and Queues are linear data structures modeling real-life scenarios. Stack models a Last In First Out scenario and the Queue models a First In First Out Scenario.

Both data structures are used to organize access to data, the difference is in the way every structure organizes that access…

800×273 18.1 KB

Push is the adding method to the stack while Pop is the method to access and delete the top element of the stack.

Enqueue is the method to add an element to a Queue, and Dequeue is to remove previously enqueued elements.

Usage

Stack

1- The UNDO functionality in text editors.
2- Compiler syntax-checking for Brackets and Braces coupling.
3- Modeling piles.
4- Supporting recursion, and keeping track of previous function calls.
5- Used in a Depth First Search on a graph or tree.

Queue

1- Modeling a waiting line.
2- Any First Come First Serve scenario, in a web server request management for example.
3- Breath first search graph or tree traversal.

Complexity

1400×976 90.9 KB

Stack

Most operations are of a constant time complexity big O, besides searching which is linear in case the item we are looking for doesn’t exist.

1400×858 90.7 KB

Queue

Similarly, only Contains and Removal operations are linear in a queue. All the other operations are of constant complexity.

Popular problems solved with Queue and Stack

BFS and DFS, mainly in trees and graphs, are the most common design patterns where queues and stacks play an essential role.

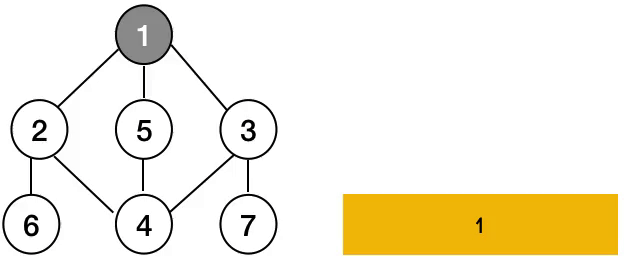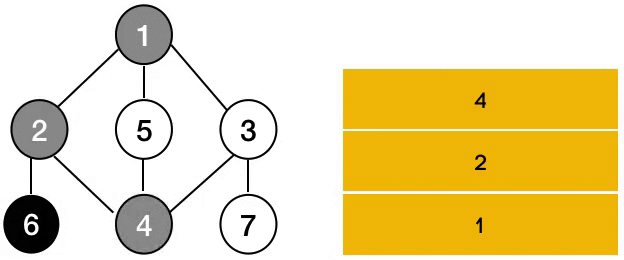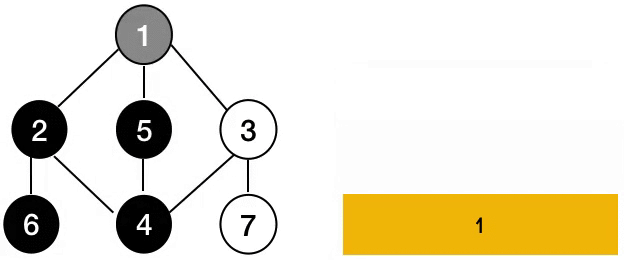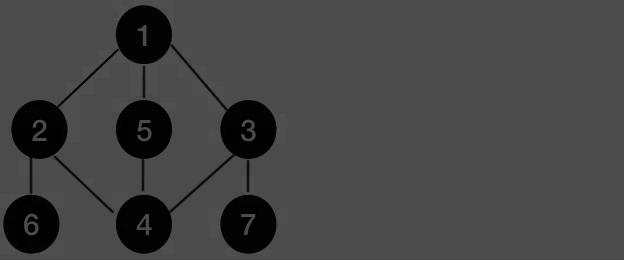
Breadth-First Search (BFS)

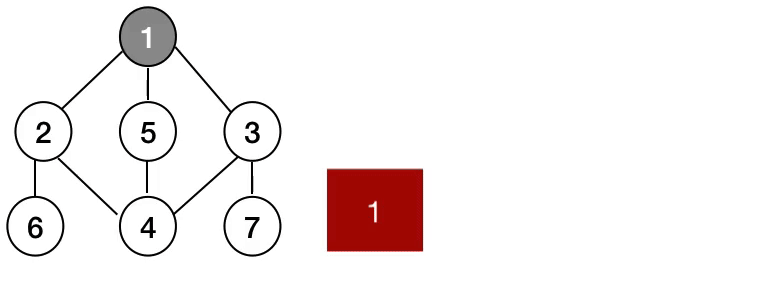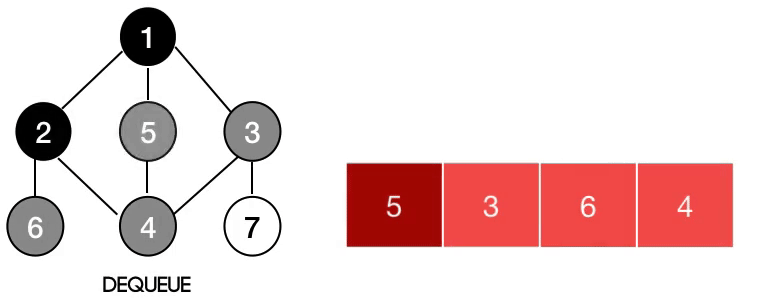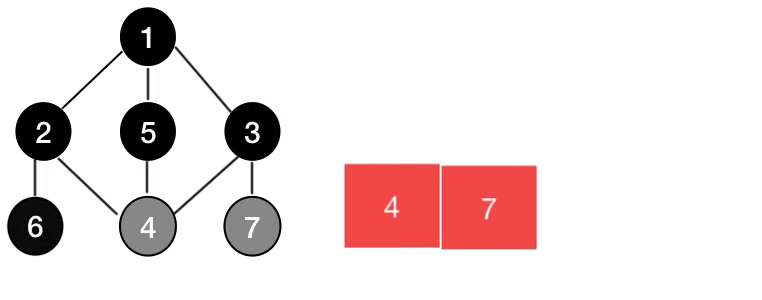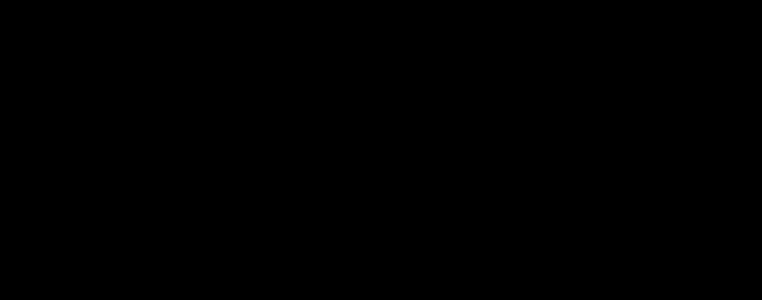
Visits all vertices or nodes in a tree level by level. In order to do so, every time we visit a node we push its children into a queue, so after we are done with that node, we will have access to the next level nodes in order.

Depth-First Search (DFS)

Visits all vertices or nodes in a tree starting by the root node and keeps visiting all child nodes until it reaches the deepest.

DFS uses a Stack in order to store the child nodes of every vertex it visits in order to revisit them after done with the deeper nodes.

#2

Stack and queue both are a linear type of data structures both are used to store data in linear fashion

The basic difference between this two is

Stack stores data in LIFO manner it means last in first out. Last element push in the stack will be pop first. Push means insert an element into the stack and pop means delete an element from the stack. All the elements insert at the top of the stack and delete at top of the stack. We can implement stack with linked list.
Queue stores data in FIFO manner it means first in first out. For example line of students for registration first come student will be registere first. It means first enqueued element Will be dequeue first. Enqueue means insert an element in the queue and dequeue means delete an element from the queue. All the elements will be interest at rear and deleted from the front. We can implement queue with linked list.