Rules for Limits
Limits are easy to evaluate if we know a few simple principles, which are listed below. All these rules are based on the known limits of two functions f(x) and g(x), when x approaches a point k:
Rules for Evaluating Limits
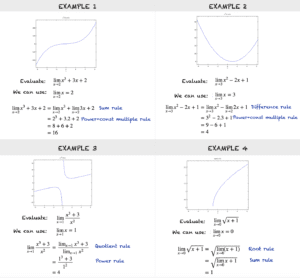
Examples of Using Rules to Evaluate Limits
Examples of Evaluating Limits Using Simple Rules
Here are a few examples that use the basic rules to evaluate a limit. Note that these rules apply to functions which are defined at a point as x approaches that point.
Limits for Polynomials
Examples 1 and 2 are that of polynomials. From the rules for limits, we can see that for any polynomial, the limit of the polynomial when x approaches a point k is equal to the value of the polynomial at k. It can be written as:
Hence, we can evaluate the limit of a polynomial via direct substitution, e.g.
lim(x→1) x^4+3x^3+2 = 1^4+3(1)^3+2 = 6
Limits for Rational Functions
For rational functions that involve fractions, there are two cases. One case is evaluating the limit when x approaches a point and the function is defined at that point. The other case involves computing the limit when x approaches a point and the function is undefined at that point.
Case 1: Function is Defined
Similar to the case of polynomials, whenever we have a function, which is a rational expression of the form f(x)/g(x) and the denominator is non-zero at a point then:
lim(x→k) f(x)/g(x) = f(k)/g(k) if g(k)≠0
We can therefore evaluate this limit via direct substitution. For example:
lim(x→0)(x^2+1)/(x-1) = -1
Here, we can apply the quotient rule or easier still, substitute x=0 to evaluate the limit. However, this function has no limit when x approaches 1. See the first graph in the figure below.
Case 2: Function is Undefined
Let’s look at another example:
lim(x→2)(x^2-4)/(x-2)
At x=2 we are faced with a problem. The denominator is zero, and hence the function is undefined at x=2. We can see from the figure that the graph of this function and (x+2) is the same, except at the point x=2, where there is a hole. In this case, we can cancel out the common factors and still evaluate the limit for (x→2) as:
lim(x→2)(x^2-4)/(x-2) = lim(x→2)(x-2)(x+2)/(x-2) = lim(x→2)(x+2) = 4
Following image shows the above two examples as well as a third similar example of g_3(x):