Phases in Calculus

Data Science, AI and ML
#1

Calculus can, therefore, be considered to comprise of two phases: cutting and rebuilding.

In mathematical terms, the cutting process always involves infinitely fine subtraction, which is used to quantify the differences between the parts. Accordingly, this half of the subject is called differential calculus. The reassembly process always involves infinite addition, which integrates the parts back into the original whole. This half of the subject is called integral calculus.

– Page xv, Infinite Powers, 2019.

With this in mind, let us revisit our simple example.

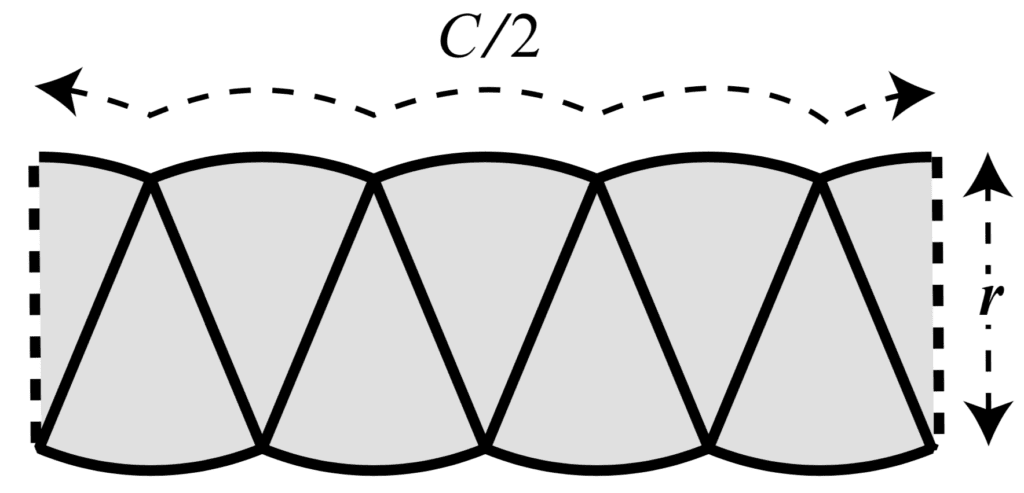
Suppose that we have sliced the circular shape of the moon into smaller pieces, and rearranged the pieces alongside one another.

The shape that we have formed is similar to a rectangle having a width equal to half the circle circumference, C/2, and a height equal to the circle radius, r.

Rearranging Slices of a Circle Into a Rectangle
Taken from Infinite Powers.

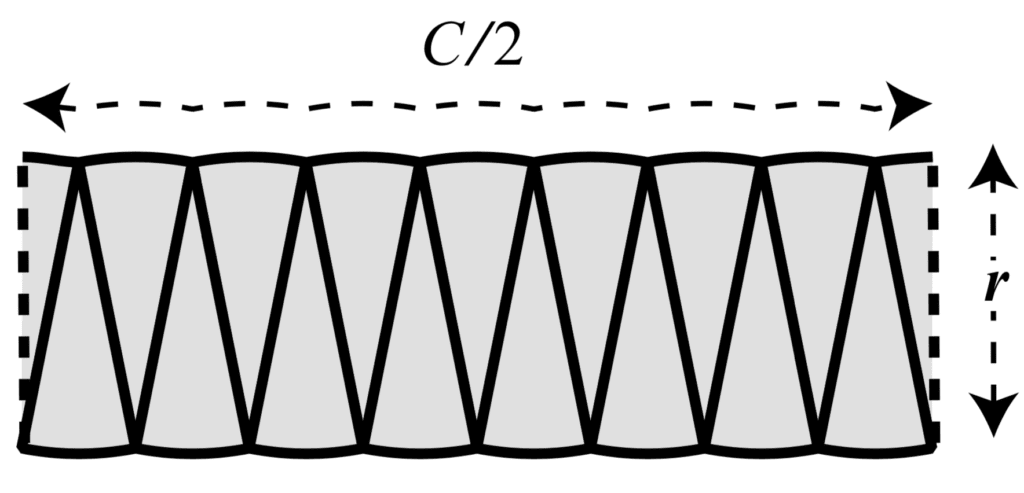
To flatten out the curvature further, we can slice the circle into thinner pieces.

Rearranging Thinner Slices of a Circle Into a Rectangle
Taken from Infinite Powers.

The thinner the slices, the more the curvature flattens out until we reach the limit of infinitely many slices, where the shape is now perfectly rectangular.

Rearranging Infinitely Thin Slices of a Circle Into a Rectangle
Taken from Infinite Powers.

We have cut out the slices from the circular shape, and rearranging them into a rectangle does not change their area. Hence, calculating the area of the circle is equivalent to calculating the area of the resulting rectangle: A = rC/2.

Curves are not only a characteristic of geometric shapes, but also appear in nature in the form of parabolic arcs traced by projectiles, or the elliptical orbits of planets around the sun.

And so began the second great obsession: a fascination with the mysteries of motion on Earth and in the solar system.

– Page xix, Infinite Powers, 2019.

And with curves and motion, the next natural question concerns their rate of change.

With the mysteries of curves and motion now settled, calculus moved on to its third lifelong obsession: the mystery of change.

– Page xxii, Infinite Powers, 2019.

It is through the application of the Infinity Principle that calculus allows us to study motion and change too, by approximating these into many infinitesimal steps.

It is for this reason that calculus has come to be considered the language of the universe.